Sorting Algorithms

Overview Table

Algorithm	Efficiency	Importance	Category	Strategy
Quick Sort	★★★★☆	★★★★★	Comparison Sort	Divide and Conquer
Merge Sort	★★★★☆	★★★★★	Comparison Sort	Divide and Conquer
Heap Sort	★★★★☆	★★★★☆	Comparison Sort	Heap Data Structure
Bubble Sort	★☆☆☆☆	★☆☆☆☆	Comparison Sort	Exchanging
Insertion Sort	★★☆☆☆	★★★☆☆	Comparison Sort	Insertion
Selection Sort	★☆☆☆☆	★★☆☆☆	Comparison Sort	Selection
Radix Sort	★★★★★	★★★★☆	Non-Comparison Sort	Distribution
Bucket Sort	★★★☆☆	★★★☆☆	Non-Comparison Sort	Distribution
Counting Sort	★★★☆☆	★★★☆☆	Non-Comparison Sort	Counting

Quick Sort

Explanation: Quick Sort is a highly efficient sorting algorithm and is based on the divide-and-conquer approach. It works by selecting a 'pivot' element from the array and partitioning the other elements into two sub-arrays, according to whether they are less than or greater than the pivot. The sub-arrays are then sorted recursively.

Time Complexity:

• Average case: O(n log n)
• Worst case: O(n^2) (rare)

Visualizations:

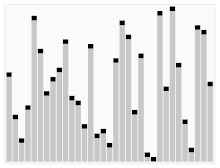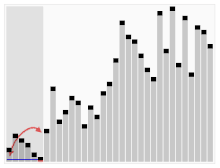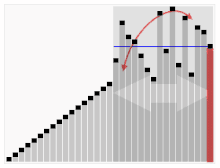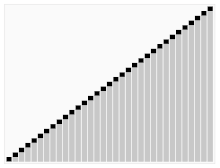
History: Quick Sort was developed by British computer scientist Tony Hoare in 1959 and has since become one of the most widely used sorting algorithms due to its efficiency and simplicity.

Code Sample:

function quickSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  const pivot = arr[Math.floor(arr.length / 2)];
  const left = arr.filter((x) => x < pivot);
  const middle = arr.filter((x) => x === pivot);
  const right = arr.filter((x) => x > pivot);
  return [...quickSort(left), ...middle, ...quickSort(right)];
}

// Example usage
const arr = [3, 6, 8, 10, 1, 2, 1];
console.log(quickSort(arr));

Merge Sort

Explanation: Merge Sort is a stable, comparison-based sorting algorithm that divides the unsorted list into n sublists, each containing one element, and then repeatedly merges sublists to produce new sorted sublists until there is only one sublist remaining.

Time Complexity:

• Best case: O(n log n)
• Worst case: O(n log n)

Visualizations:

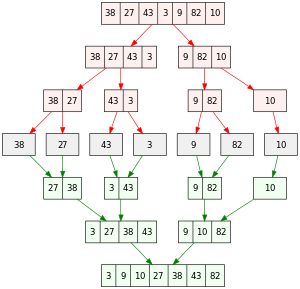
History: Merge Sort was invented by John von Neumann in 1945. It is known for its efficiency and is often used in situations where stability is important.

Code Sample:

function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));
  return merge(left, right);
}

function merge(left, right) {
  const result = [];
  let i = 0,
    j = 0;
  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) {
      result.push(left[i]);
      i++;
    } else {
      result.push(right[j]);
      j++;
    }
  }
  return result.concat(left.slice(i)).concat(right.slice(j));
}

// Example usage
const arr = [3, 6, 8, 10, 1, 2, 1];
console.log(mergeSort(arr));

Heap Sort

Explanation: Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure. It first builds a max-heap from the input data and then repeatedly extracts the maximum element from the heap and rebuilds the heap until all elements are sorted.

Relies on the Heap Data Structure for sorting.

Time Complexity:

• Best case: O(n log n)
• Worst case: O(n log n)

Visualizations:

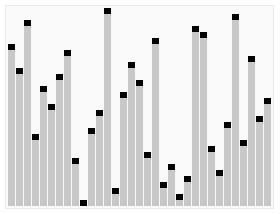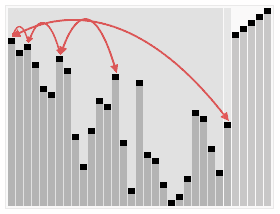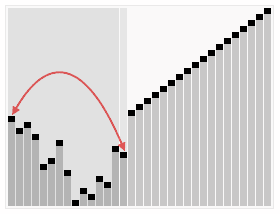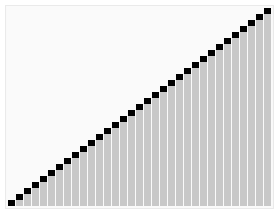
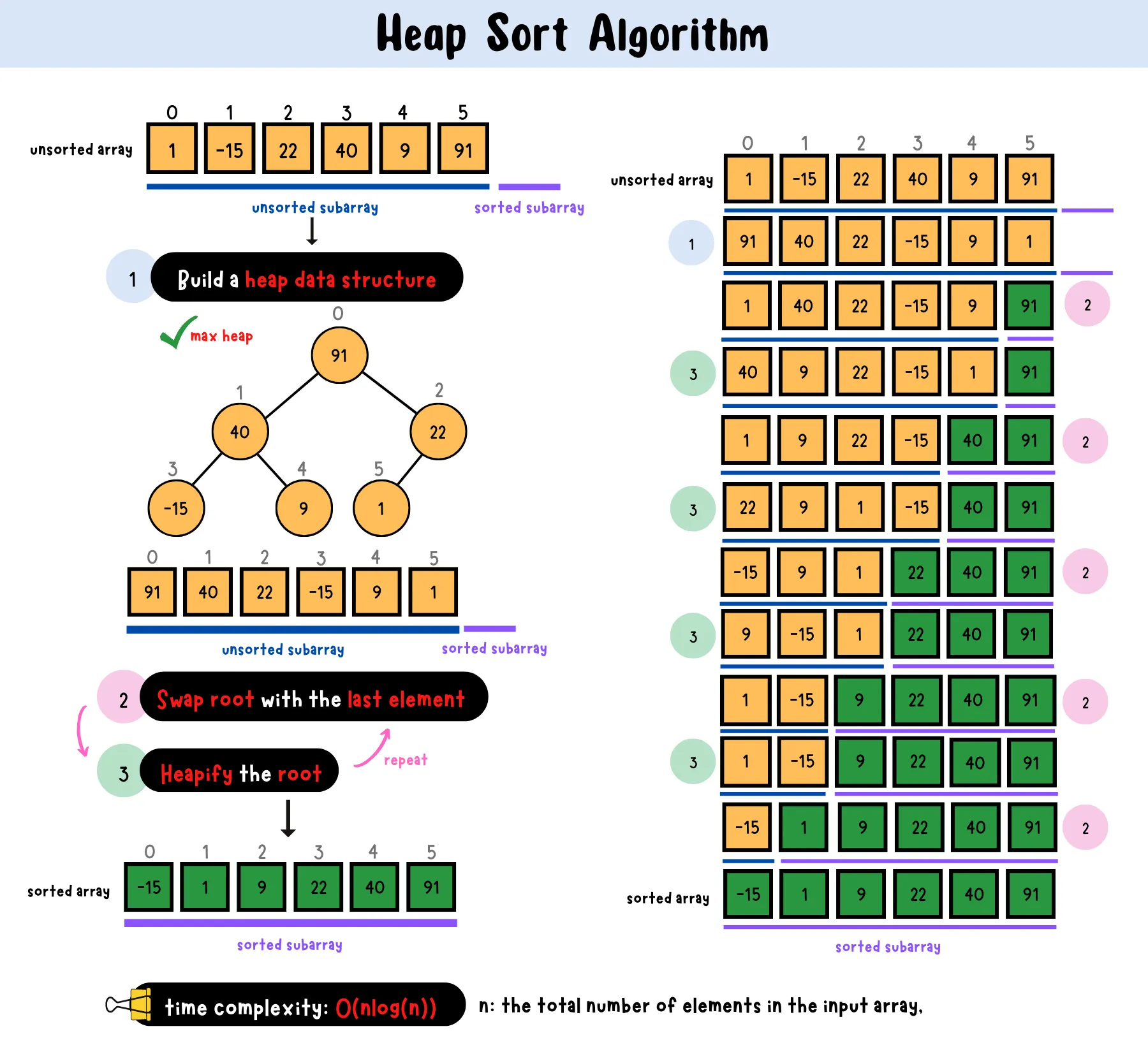
History: Heap Sort was introduced by J.W.J. Williams in 1964 as a method for sorting using the heap data structure. It is known for its good performance in the worst-case scenario.

Code Sample:

function heapify(arr, n, i) {
  let largest = i;
  const left = 2 * i + 1;
  const right = 2 * i + 2;

  if (left < n && arr[left] > arr[largest]) {
    largest = left;
  }

  if (right < n && arr[right] > arr[largest]) {
    largest = right;
  }

  if (largest !== i) {
    [arr[i], arr[largest]] = [arr[largest], arr[i]];
    heapify(arr, n, largest);
  }
}

function heapSort(arr) {
  const n = arr.length;

  for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
    heapify(arr, n, i);
  }

  for (let i = n - 1; i > 0; i--) {
    [arr[0], arr[i]] = [arr[i], arr[0]];
    heapify(arr, i, 0);
  }
}

// Example usage
const arr = [3, 6, 8, 10, 1, 2, 1];
heapSort(arr);

Bubble Sort

Explanation: Bubble Sort is a simple comparison-based algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The pass through the list is repeated until the list is sorted.

Time Complexity:

• Best case: O(n)
• Worst case: O(n^2)

Visualizations:

History: Bubble Sort is one of the simplest sorting algorithms and has been used since the early days of computer science. However, due to its inefficiency, it is rarely used in practice.

Code Sample:

function bubbleSort(arr) {
  const n = arr.length;
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
}

// Example usage
const arr = [3, 6, 8, 10, 1, 2, 1];
bubbleSort(arr);

Insertion Sort

Explanation: Insertion Sort is a simple sorting algorithm that builds the final sorted array one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort.

Time Complexity:

• Best case: O(n)
• Worst case: O(n^2)

History: Insertion Sort has been known since at least the mid-20th century. It is useful for small data sets or as part of more complex algorithms.

Code Sample:

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    const key = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = key;
  }
}

// Example usage
const arr = [3, 6, 8, 10, 1, 2, 1];
insertionSort(arr);

Selection Sort

Explanation: Selection Sort is an in-place comparison-based algorithm. It has O(n^2) time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort.

Time Complexity:

• Best case: O(n^2)
• Worst case: O(n^2)

History: Selection Sort is one of the oldest sorting algorithms and has been used since the early days of computing. It is mainly of academic interest today.

Code Sample:

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let minIdx = i;
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[j] < arr[minIdx]) {
        minIdx = j;
      }
    }
    [arr[i], arr[minIdx]] = [arr[minIdx], arr[i]];
  }
}

// Example usage
const arr = [3, 6, 8, 10, 1, 2, 1];
selectionSort(arr);
console.log(arr);

Radix Sort

Explanation: Radix Sort is a non-comparative sorting algorithm. It sorts numbers by processing individual digits. It is efficient for sorting large lists of integers or strings.

Time Complexity:

• Best case: O(nk)
• Worst case: O(nk), where k is the number of digits

Visualizations:

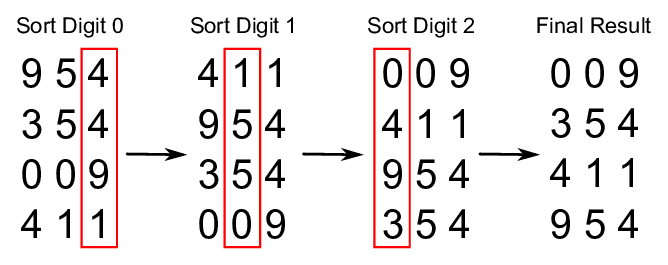
History: Radix Sort was introduced by Herman Hollerith in 1887. It is particularly useful for sorting data with a large range of values.

Code Sample:

function countingSort(arr, exp) {
  const n = arr.length;
  const output = new Array(n).fill(0);
  const count = new Array(10).fill(0);

  for (let i = 0; i < n; i++) {
    const index = Math.floor(arr[i] / exp) % 10;
    count[index]++;
  }

  for (let i = 1; i < 10; i++) {
    count[i] += count[i - 1];
  }

  for (let i = n - 1; i >= 0; i--) {
    const index = Math.floor(arr[i] / exp) % 10;
    output[count[index] - 1] = arr[i];
    count[index]--;
  }

  for (let i = 0; i < n; i++) {
    arr[i] = output[i];
  }
}

function radixSort(arr) {
  const max = Math.max(...arr);
  for (let exp = 1; Math.floor(max / exp) > 0; exp *= 10) {
    countingSort(arr, exp);
  }
}

Bucket Sort (Bin Sort)

Explanation: Bucket Sort works by distributing elements into several buckets, then sorting each bucket individually using another sorting algorithm or recursively applying the bucket sort. It is a cousin of radix sort.

Time Complexity:

• Best case: O(n + k)
• Worst case: O(n^2) (depends on the sorting algorithm used inside the buckets and the distribution of the input)

History: Bucket Sort is often attributed to Harold H. Seward in 1954 and is used for sorting numbers uniformly distributed over a range.

Code Sample:

function bucketSort(arr, bucketSize = 5) {
  if (arr.length === 0) {
    return arr;
  }

  let i,
    minValue = arr[0],
    maxValue = arr[0];

  // Determine minimum and maximum values
  arr.forEach((currentVal) => {
    if (currentVal < minValue) {
      minValue = currentVal;
    } else if (currentVal > maxValue) {
      maxValue = currentVal;
    }
  });

  // Initialize buckets
  const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
  const buckets = new Array(bucketCount);

  for (i = 0; i < buckets.length; i++) {
    buckets[i] = [];
  }

  // Distribute input array values into buckets
  arr.forEach((currentVal) => {
    buckets[Math.floor((currentVal - minValue) / bucketSize)].push(currentVal);
  });

  // Sort each bucket and concatenate the results
  arr.length = 0;
  buckets.forEach((bucket) => {
    insertionSort(bucket);
    bucket.forEach((element) => {
      arr.push(element);
    });
  });

  return arr;
}

// Helper function: Insertion Sort
function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    const key = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = key;
  }
}

// Example usage
const arr = [3.2, 0.4, 2.7, 1.6, 0.9, 2.3, 3.0];
console.log(bucketSort(arr));

Counting Sort

Explanation: Counting Sort is a non-comparative sorting algorithm that sorts elements by counting the number of occurrences of each unique element in the input array. The count is stored in an auxiliary array and then used to place the elements in the correct position in the output array. It is efficient for sorting integers with a known, limited range.

Time Complexity:

• Best case: O(n + k)
• Worst case: O(n + k) (where n is the number of elements and k is the range of the input)

History: Counting Sort was introduced by Harold H. Seward in 1954. It is mainly used for sorting integers and is particularly effective for small ranges.

Code Sample:

function countingSort(arr) {
  const max = Math.max(...arr);
  const min = Math.min(...arr);
  const range = max - min + 1;

  const count = new Array(range).fill(0);
  const output = new Array(arr.length);

  // Count occurrences of each element
  arr.forEach((num) => {
    count[num - min]++;
  });

  // Compute cumulative count
  for (let i = 1; i < count.length; i++) {
    count[i] += count[i - 1];
  }

  // Place the elements in sorted order
  for (let i = arr.length - 1; i >= 0; i--) {
    output[count[arr[i] - min] - 1] = arr[i];
    count[arr[i] - min]--;
  }

  // Copy the sorted elements back to the original array
  for (let i = 0; i < arr.length; i++) {
    arr[i] = output[i];
  }

  return arr;
}

// Example usage
const arr = [4, 2, 2, 8, 3, 3, 1];
console.log(countingSort(arr));

Comments

Recent Work

Basalt

basalt.software

Free desktop AI Chat client, designed for developers and businesses. Unlocks advanced model settings only available in the API. Includes quality of life features like custom syntax highlighting.

Learn More

BidBear

bidbear.io

Bidbear is a report automation tool. It downloads Amazon Seller and Advertising reports, daily, to a private database. It then merges and formats the data into beautiful, on demand, exportable performance reports.

Learn More